SIFAT-SIFAT STRUKTUR VARIOGRAM

2.1  Perilaku variogram dekat titik awal

Kontinuaitas satu ketergantungan variabel sangat erat hubungannya dengan perilaku suatu semivariogram di dekat titik awal.

h   g(h)	Gambar 4. Suatu perilaku parabolik di dekat titik awal memperlihatkan suatu kontinuitas variabel yang tinggi, yaitu sifat data yang teratur, seperti variabel geofisika, geo-kimia, atau kadang-kadang data tebal.
h   g(h)	Gambar 5. Perilaku linier dakat titik awal menyata-kan suatu variabel dengan kontinuitas sedang. Variogram semacam ini biasa-nya berlaku pada data kadar bijih.
h   g(h)	Gambar 6. Variabel dengan ketidakteraturan yang tinggi  akan memberikan variogram yang diawali dengan lompatan. Ketidak-kontinuan ini dinamakan dengan nugget effect .
h   g(h)	Gambar 7. Suatu semivariogram yang berperilaku horisontal adalah hasil dari perhitungan variabel dengan distribusi acak.

2.2       Daerah pengaruh (range)

Secara umum g(h) akan naik dengan bertambahnya harga h, artinya besarnya perbedaan harga pada dua titik akan sangat tergantung dengan jarak ke dua titik tersebut.

Kenaikan harga g(h) tersebut akan berlangsung selama masih terdapat pengaruh harga antar titik, daerah ini dikenal dengan daerah pengaruh suatu conto, sampai akhirnya konstan di suatu harga g(¥) = C (sill) yang merupakan varians populasi (varians a priori).

Daerah pengaruh suatu conto ini mempunyai suatu jarak dengan notasi a yang dikenal dengan nama daerah pengaruh (range). Di luar jarak ini maka rata-rata variasi harga Z(x) dan Z(x+h) tidak lagi tergantung dengan jarak, dengan kata lain Z(x) dan Z(x+h) tidak berkolerasi satu dengan yang lainnya. Range a adalah suatu ukuran untuk daerah pengaruh.

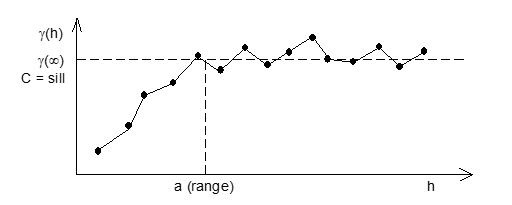
(Semi) variogram mis. ketebalan suatu endapan berlapis

2.3       Struktur bersarang (nested structure)

Jika pada suatu endapan bahan galian terdapat beberapa struktur yang berbeda, maka untuk setiap struktur akan memberikan variogram dengan harga a yang berbeda (ukuran untuk perbedaan dimensi struktur) dan harga sill yang berbeda (ukuran untuk rata-rata simpangan variabel).

Pengaruh-pengaruh struktur ini akan saling tumpang tindih sehingga akan memberikan satu variogram gabungan, yang bisa diuraikan atas komponen-komponennya (Gambar 9).

Variogram-variogram semacam ini biasanya akan muncul pada endapan fluviatil, seperti endapan  bentuk lensa yang saling tumpang tindih atau fingering.

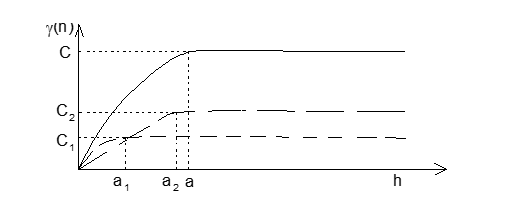
Struktur bersarang (nested structure) suatu contoh teoritis

2.4       Nugget variance dan struktur mikro

Variogram dengan struktur bersarang umumnya terbentuk jika jarak pasangan antar conto sangat kecil dibandingkan dengan range a .

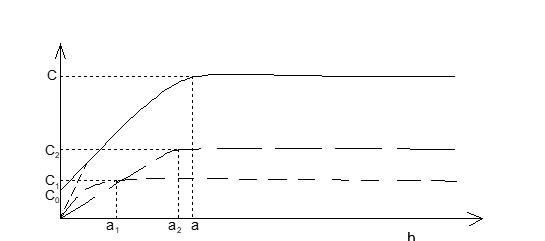
Nugget variance dan struktur mikro

Pengaruh dari struktur mikro terhadap pemilihan jarak antar pasangan antar conto ini akan terlihat dengan muncul tidaknya nugget variance. Nugget effect ini bisa dihindarkan dengan memperkecil jarak h.

Adanya nugget variance ini juga bisa diakibatkan oleh kesalahan pada analisa.

2.5       Anisotropi

Mengingat h merupakan suatu vektor, maka suatu variogram harus ditentukan untuk berbagai arah. Suatu penyelidikan perubahan g(h) sesuai dengan arah orientasinya memungkinkan munculnya anisotropi.

a.   Isotropi

Jika variogram-variogram pada berbagai arah sama, maka dapat diartikan bahwa g(h) merupakan suatu fungsi dari harga absolut vektor

, jika h₁, h₂, dan h₃ adalah komponen-komponen vektor .

b.   Anisotropi geometri

Jika pada beberapa g(h) dengan arah yang berbeda tetap mem-punyai harga sill C dan nugget variance yang sama, sedangkan kenaikan variogram-variogram yang dinyatakan dengan harga range a  berbeda, maka akan terlihat apa yang disebut dengan anisotropi geometri.

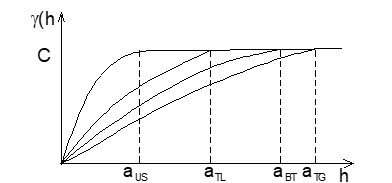
a_US      :           range pada arah Utara-Selatan

a_TL       :           range pada arah Timurlaut-Baratdaya

a_BT      :           range pada arah Timur-Barat

a_TC      :           range pada arah Baratlaut-Tenggara

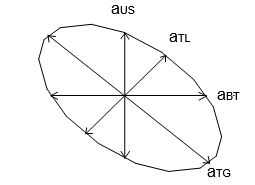
Umumnya semua besaran range a tersebut akan tersebar menuruti bentangan elipsoida. Kondisi seperti ini sering dijum-pai pada endapan placer  (mis. endapan pasir besi pantai).

Anisotropi geometri

c.   Anisotropi zonal

Dalam beberapa hal mungkin dijumpai bahwa variogram pada arah tertentu sangat berbeda sekali mis. pada endapan bahan galian yang mempunyai struktur perlapisan, dimana variasi kadar pada arah tegak lurus terhadap bidang perlapisan sangat besar dibandingkan variasinya pada bidang perlapisannya.

Pada kasus ini model variogramnya benar-benar anisotrop sempurna dan dapat diuraikan sebagai berikut :

horizontal   vertikal   C2   g2   h   C1   komponen isotrop              dan suatu komponen anisotrop             murni yang diperoleh dari             variogram arah tegaklurus             bidang perlapisan                                          g2(h3)

C1   g1

Anisotropi zonal

sehingga diperoleh :

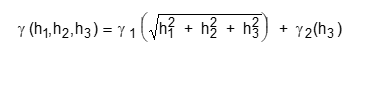
2.6       Propotional effect

Dalam banyak hal varians pada suatu daerah sangat tergantung dengan harga rata-rata lokal. Hal ini bisa dilihat dari hubungan antara varians daerah tertsebut (mis. kelompok data bor) dengan harga rata-rata kuadrat.

0,10   0,30   0,20   s2     2,0   1,5   1,0   h   150′   100′   50′   level 2   level 1   g(h)
Gambar 13.     Hubungan antara varians dan rata-rata lokal untuk endapan                           molibdenit, serta variogram tiap level yang mempunyai g(¥)                           dengan besar yang berbeda.

Jika hubungan antara varians dan rata-rata kuadrat lokal tersebut linier, maka akan bisa ditentukan variogram relatifnya, yaitu setiap tahap pada perhitungan variogram eksperimentalnya harus dibagi dengan kuadrat harga rata-rata lokal sebagai berikut :

dengan

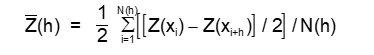
sehingga diperoleh satu variogram relatif berikut ini :

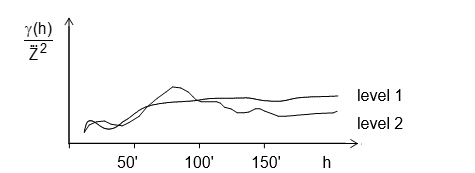
Kisaran variogram relatif

Gejala efek proportional ini umumnya dijumpai pada data yang mempunyai distribusi log normal .

2.7       Drift

Kondisi ini dijumpai pada suatu variogram yang pada awalnya berperilaku normal, yaitu naik sampai mencapai sill, tetapi selanjutnya naik secara mendadak secara parabolik. hal ini berarti, bahwa variabel terregionalnya tidak lagi stationer.

Drift ini dapat dengan mudah diketahui jika dihitung perbedaan rata-ratavariabel pada x₁ dan x_i+h sesuai dengan arah vektor h nya :

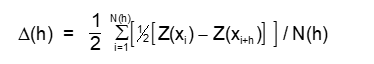
dan ditampilkan secara grafis.

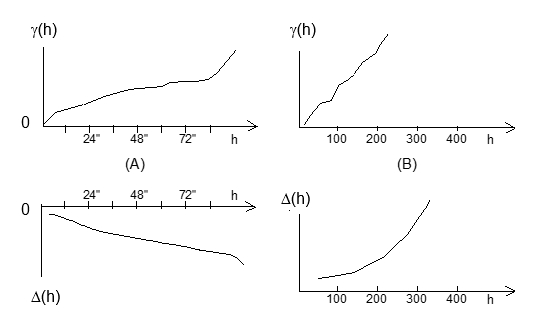
Contoh efek parabolik suatu drift pada variogram dari data                                                                       sulfur pada tambang batubara (A) dan data timbal pada                                                                         tambang Pb-Zn (B )

2.8       Hole effect

Dalam hal variogram dihitung sepanjang data yang mempunyai harga tinggi dan kemudian rendah (mis. data kadar pada alur yang memotong beberapa urat bijih), maka setelah mencapai sill variogram yang diperoleh akan naik atau turun secara periodik. Berikut ini diperlihatkan contoh hole effect dari CLARK and JOURNELL & HUIJBREGTS.

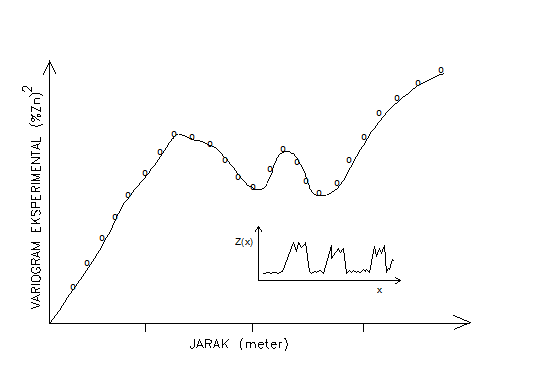
Contoh variogram dengan hole effect 

2.9       Support        

Suatu variabel terregional akan tergantung pada suatu daerah ruang tertentu atau suatu bidang/daerah geometrik tertentu sesuai dengan variasi variabel tersebut. Selain daripada itu variabel-variabel tersebut juga terikat pada support geometrik yang dikontrol oleh volume, bentuk, serta orientasinya. Jika support ini berubah, maka akan terdefinisi suatu variabel terregional baru.

Dengan pembesaran support akan terbentuk regularisasi. Semakin besar support geometrik, akan semakin sama sifat variabel terregional dalam suatu endapan /ruang.

Antar variogram-variogram dengan bermacam-macam support geo-metrik terdapat hubungan sederhana, sedemikian sehingga variogram conto bentuk titik dapat dianggap sebagai variogram conto. Demikian pula variogram volume yang lebih besar dapat didekati dengan variogram volume yang lebih kecil.

Pada prakteknya, suatu variogram eksperimen untuk conto tidak sama dengan variogram titik yang dimiliki oleh titik-titik ruang. Karena support geometri suatu conto (conto inti, conto alur, hand spacimen, ..) sangat kecil, kita dapat langsung menggunakan variogram conto.

3.         MODEL-MODEL VARIOGRAM

Seperti halnya pada suatu histogram dapat dibuatkan model matematiknya seperti distribusi normal dll., maka pada variogram eksperimental juga dapat dibuatkan model matematiknya yang akan bermanfaat untuk perhitungan selanjutnya.

Pemilihan model ini dipengaruhi oleh beberapa hal tersebut di bawah ini :

a.    Perilaku variogram dekat titik awal, perilaku ini biasanya mudah dikenali. ada tidaknya nugget variance dapat diperoleh dengan eksploitasi g(h) memotong sumbu tegak (untuk h=0)

b.    Kehadiran sill, pada awalnya varians statistik dari data dapat dianggap sebagai harga sill.

c.     Kehadiran anisotropi, struktur bersarang dll.

Berdasarkan hadir tidaknya sill dan range tersebut, maka model semivariogram dikelompokan menjadi model dengan sill dan model tanpa sill.

3.1       Model dengan sill

Model dengan sill ini meliputi :

a.         Berperilaku linier dekat titik awal

            Model sferis (model MATHERON) :

           

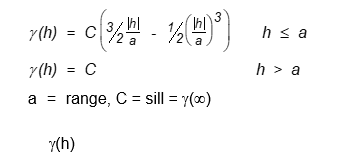
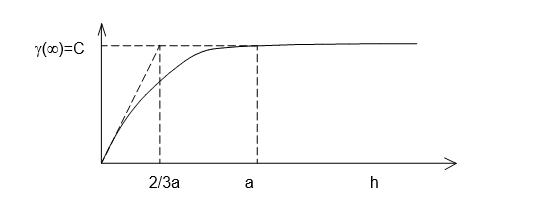
Variogram model sferis

b.         Berperilaku linier dekat dengan titik awal

            Model eksponensial (model FORMERY) :

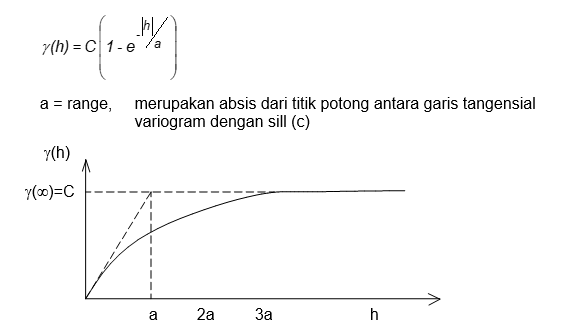
            Variogram model eksponensial

c.         Berperilaku parabolik di dekat titik awal

            Model Gaussian  :

      

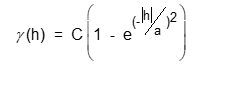
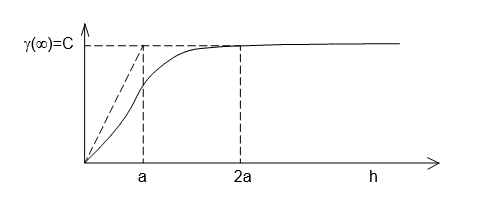
Variogram model parabolik

3.2       Model tanpa sill

Model tanpa sill meliputi  :

a.         Model Linier :            g (h) = pçh ê^l

                                    dimana :         p adalah konstanta yang ditetapkan dan

                                                                                    0<l<2 jika l =2, maka akan menjadi model parabola.

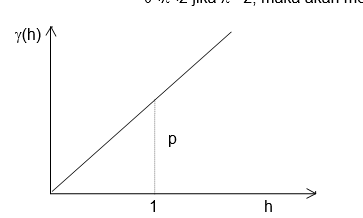
            Gambar 20.  Variogram model linier

b.         Model logaritmik atau de Wijsian :

                        g (h) = 3a log çh ê + B

            dimana ;         B= Co + 3a(3/2 – log l )

                                    a adalah konstanta yang ditetapkan

                                    l  adalah panjang ekivalen conto.

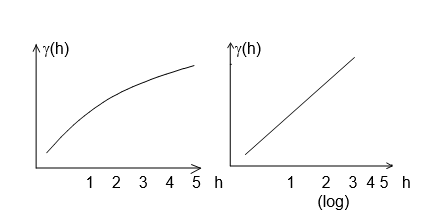
            Variogram model parabolik